Day25:Dynamic Programming(DP) - 动态规划(上)

在认识动态规划之前先来理解Divide and Conquer(分治法)吧!Divide and Conquer是一种演算法，执行的步骤如下

1. Divide:先将大问题不断切割成小问题
2. Conquer:用递回的方式处理所有的子问题
3. Combine:将所有的结果合并起来就是最终解答

动态规划的概念与Divide and Conquer的概念相似，会将大问题切割成多个小问题，再将小问题的解答组合起来，不过有些小问题其实是重复的，所以会发生重复计算的问题，这时候动态规划就会把已经计算过的答案存起来，用空间换取时间，加速执行时间，这就是动态规划的核心精神所在。

斐波那契数列

斐波那契数列由0和1开始，之後的斐波那契数列就是由前两位数字相加而得出 ，也就是第n项为第n-1和第n-2项的总和 - 引用自wikipedia

图片来源:https://www.mathsisfun.com/numbers/fibonacci-sequence.html
ex. 89 = 55+34 (n11 = n10 + n9)

下图是斐波那契数列递回执行的流程图，每个方格都是一个函式，观察下图就会发现有不少重复计算的现象，因此时间复杂度为O(2ⁿ)。

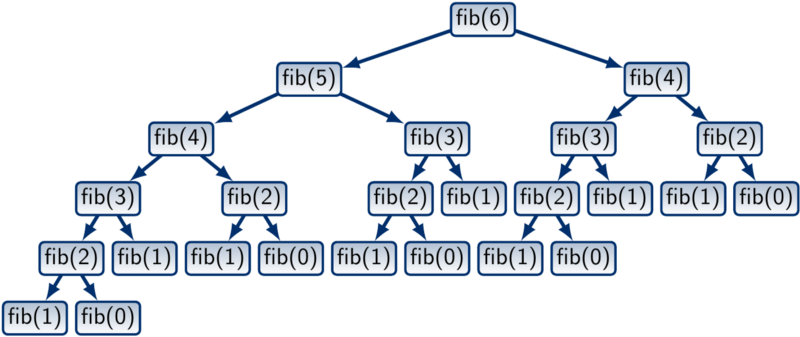
图片来源:https://tarjotin.cs.aalto.fi/CS-A1140/2020/notes/dynprog-dp.html

用js实作如下

const fibonacci = (i) => {
    if (i === 0 || i === 1) return i;
    return fibonacci(i - 1) + fibonacci(i - 2);
};

fibonacci(5);

而下图是Dynamic Programming执行的流程，因为蓝色区块已经计算过，并将计算结果暂存起来，所以黄色的区块不需要重复计算，时间复杂度为O(n)。

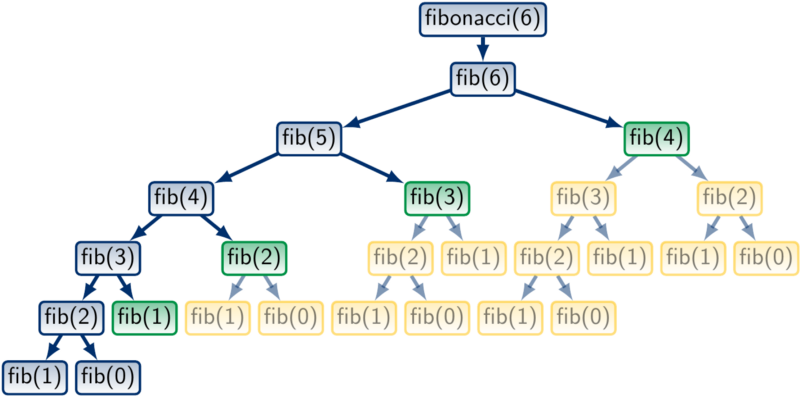
图片来源:https://tarjotin.cs.aalto.fi/CS-A1140/2020/notes/dynprog-dp.html

为甚麽称为动态规划?

因为宣告存放计算结果的阵列长度是随着输入的长度变化，存放的方式又分为两种 Bottom Up和Top Down

• Bottom Up : 使用回圈，执行顺序是由下至上，又称为Tabulation，可以想成是从小的问题开始计算，逐步计算到最终要求的值，缺点是可能会计算到没有用到的子问题。

• Top Down : 使用递回，执行顺序是由上至下，计算过的结果会存起来不会重复计算，这个方法也被称作memoization，由於递回的执行效率相较於回圈会来的差，因此这种方法会比Bottom Up还要慢，可能会有递回过深的问题。

用js实作Bottom Up

const fibonacci = (n) => {
    let temp = new Array(n);
    temp[0] = 0;
    temp[1] = 1;
    for (let i = 2; i < n; i++) {
      temp[i] = temp[i-1] + temp[i-2];
    }
    return temp[n-1] + temp[n-2]
  }

  fibonacci(6);//输出8

用js实作Top Down

const fibonacci = (n) => {
    return helper(n, new Array(n));
};
const helper = (i, temp) => {
    if (i === 0 || i === 1) {
        return i;
    }
    if (!temp[i]) {
        temp[i] = helper(i - 1, temp) + helper(i - 2, temp);
    }
    return temp[i];
};

fibonacci(6); //输出8

两者的差异比较如下

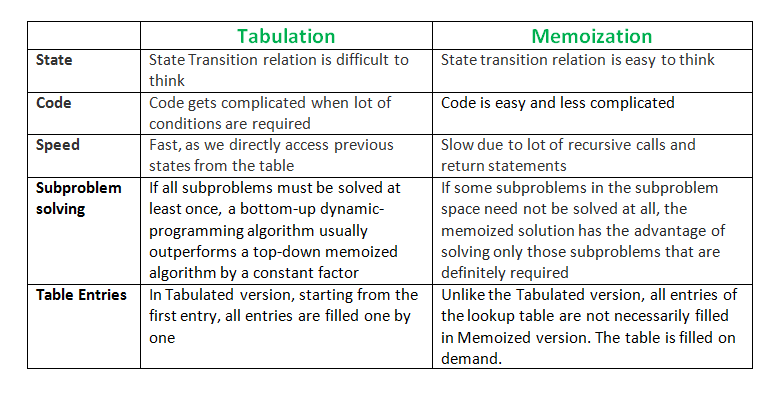
图片来源:https://www.geeksforgeeks.org/tabulation-vs-memoization/

动态规划适用的情境

1. 最佳子结构 (Optimal Substructure):问题的最佳解可以从子问题的最佳解推算出来。
2. 重叠子问题 (Overlapping Sub-problems):如斐波那契数列出现重复子问题的情形，动态规划的优势是可以储存过计算过的结果，再次遇到相同子问题的时候直接取出储存的结果，无需重复计算。
3. 无後效性(no aftereffect):即子问题的解一旦确定，就不再改变，不受在这之後、包含它的更大的问题的求解决策影响。

参考资料:dynamic-programming-laughlin-lunch-and-learn
tabulation-vs-memoization
Overlapping Subproblems Property in Dynamic Programming
动态规划