Day 21 ：广度优先搜寻 Breadth-First search(BFS)

说到广度优先搜寻我一定要现知道Queue

Queue(伫列)是先进来的元素先出去(First In First Out = FIFO)的资料结构，通常用於让程序具有排队功能，依序执行工作，

而BFS使用queue来确保先被拜访到的结点(Node)，就先成为新的搜寻起点。
以树(tree)来说会把同一层(level)的节点拜访完，再继续向下一层搜寻，直到拜访完所有节点(queue被清空为止)。

我们继续拿DFS的图为例
我们预期得到的结果是[ A, B, C, D, E, F, G, H, I, J, K]

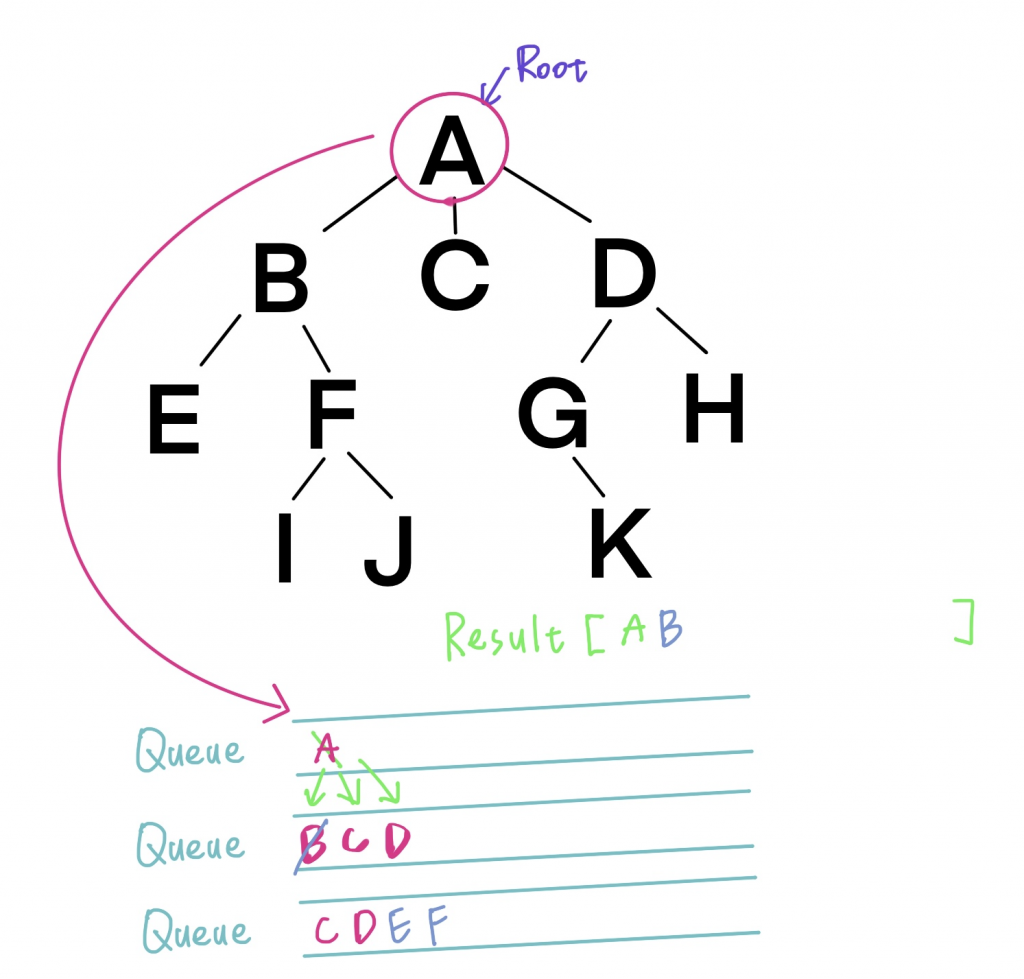
我们来看图说故事，我们先准备Queue来让我们的节点排队，然後预备一个阵列来记录结果。

首先，我们在根(Root)，也就是A开始拜访。
我们让A加入到我们的Queue，
这时候我们发现 「ㄟ～有人在排队耶」！
於是我们就把它取出来，取出来却发现他被三个小朋友给抓住了，分别是ＢＣＤ。
我们从左边开始优先，就把ＢＣＤ加到了Queue。
最後A加到我们摆放结果的地方，结束第一回合。

接着我们来到Queue的头，取出B，按照上面的方式，确认他有没有被任何小朋友抓住，同样动作：
加入Queue然後B再放入结果...

这就是我们即将用程序码实作的流程，在实作之前，我们先来看一下时间复杂度：Ｏ(V+E) ，其中V是树的节点树，E则是边数。为什麽？
我们理所当然要拜访V个点，那E呢？
想想看我们要把一个点的小朋友都加到Queue中，那如果Ａ的小朋友直接就是ＢＣＤ我们是不是就要确认ＢＣＤ是不是有小朋友，并把他们加到Queue，那如果像是I没有小朋友了(没有edge) ，我们是不是就不需要再去做loop检查的动作？
而空间复杂度:O(V)，有两个原因：分别是储存的结果 和 Queue(考虑最糟情况 有可的A下面刚好长满B~K)

而今天的题目其实就是利用一样的逻辑来实作，差别只是我们要另外把同一层的整理成一个array。
以下就是程序码的实作

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[][]}
 */
 
var levelOrder = function(root) {
if (!root) return [];

  const res = [];
  const q = [];
  q.push(root);

  while(q.length) {
    const lvl = [];
    const size = q.length;

    for (let i = 0; i < size; i++) {
      const node = q.shift();
      lvl.push(node.val);
      if (node.left) q.push(node.left);
      if (node.right) q.push(node.right);
    }
    res.push(lvl);
  }
  return res;
};

明日题目预告：验证二元搜寻树Validate Binary Search Tree
讲了几天的树，当然不可以忽略这一题！