线性回归(Linear Regression)

今日学习目标

• 认识线性回归
  • 透过机器学习来找出一条函式，来最佳化模型
  • 两种求解方法
• 线性回归程序手把手
  • 简单线性回归、多元回归、非线性回归

认识线性回归

线性回归是统计上在找多个自变数和依变数之间的关系所建出来的模型。只有一个自变数(x)和一个依变数(y)的情形称为简单线性回归大於一个自变数(x1,x2,...)的情形称为多元回归。

一个简单线性回归: y=ax+b，其中 b：截距(Intercept)，a：斜率(Slope) 为 x 变动一个单位 y 变动的量，如下图:

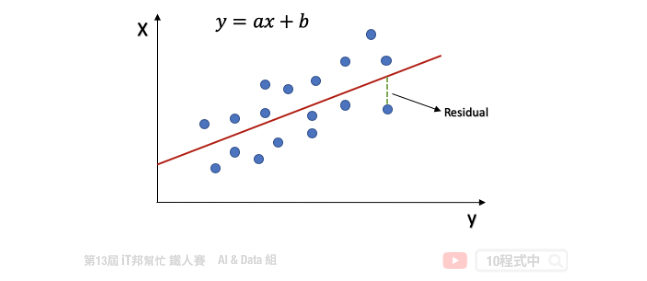
回归分析的目标函数或称损失函数(loss function)就是希望找到的模型最终的残差越小越好，来找参数 a 和 b。

两种求解方法

线性模型最常见的解法有两种，分别为 Closed-form (闭式解) 与梯度下降 (Gradient descent)。当特徵少时使用 Closed-form 较为适合，使用下面公式来求出 θ 值。我们又可以说线性模型的最小平方法的解即为 Closed-form。若当是复杂的问题时 Gradient descen 较能解决，其原因是大部分的问题其实是没有公式解的。我们只能求出一个函数 f(x) 使其误差最小越好。

• Closed-form
  

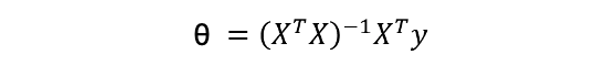
• Gradient descent
  

Least Square Method (最小平方法)

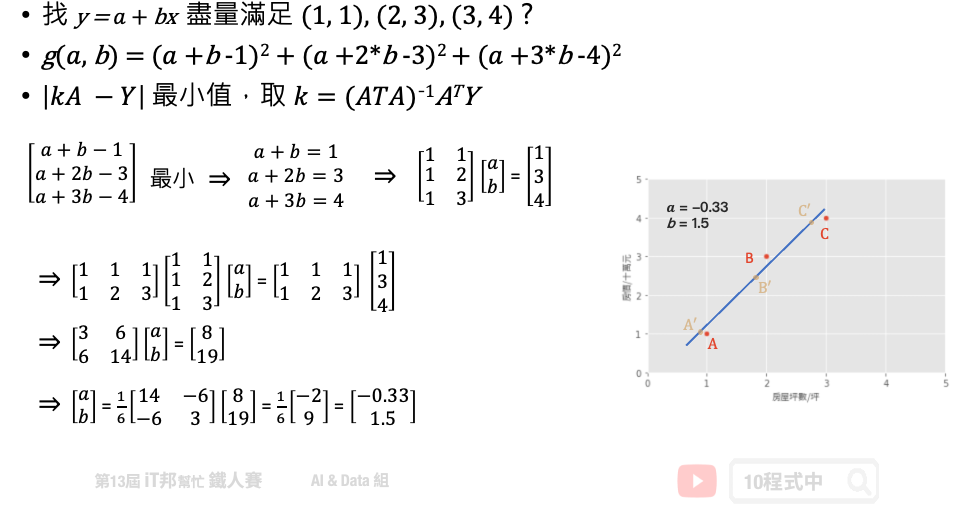
假设一个地区的房价与坪数是呈线性关系，并以下图中的三个点表示。如果我们想透过房子的坪数来预测房价，那麽我们的目标就是找到一条直线，并与座标平面上这三个点的差距越小越好。那这条直线该怎麽找呢？首先我们随机找一条直线，并计算这三点的 loss。损失函数可以自己定义，假设我们使用 MSE 均方误差来计算。透过一系列计算我们得到一个 loss 即为 MSE 值。接着我们将这个直线稍稍的转一个角度後又可以计算一个新的 MSE，此刻我们可以发现 MSE 值又比刚刚更小了。也就是说这一条新的直线能够更法应出训练集中 A、B、C 的数据点所反映的房屋坪数与房价之间的线性关系。

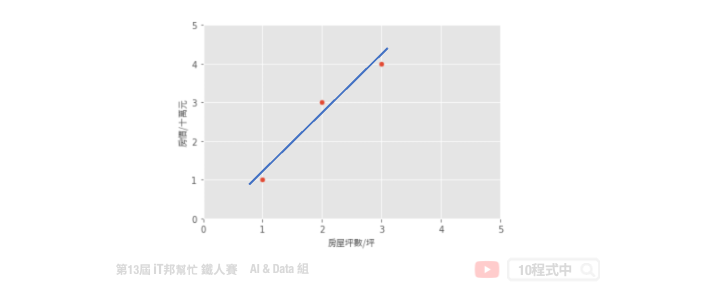
简单来说我们在一个二维空间中，我们可以找到无数条直线。现在我们能做的事情就是从这无数条直线中选出一条最佳的当作我们的预测模型，同时它面对这三点的误差是要最小的。因此我们的目标就是要最小化 MSE 也就是所谓的损失函数 (loss function)。所以整个线性回归的目标就是最小化我们的损失函数，其中一个解法就是最小平方法。因为 MSE 等於 1/n 倍的残差平方和 (RSS)，其中分母 n 为常数，不影响极小化故拿掉。因此最终的求解是满足最小化平方和，使其最小化。经过数学推导後，简化的公式如下：

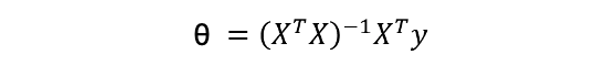
小试身手

基於上面的公式我们想找出一组参数权重 θ。也就是下图问题中的 a (θ0)、b (θ1) 两参数，使得平面上这三点平方和有极小值。这个函式对 θ0, θ1 偏做微分设他们为0，接着我们对方程序求解。 此函式只有极小值，因此我们得到的 θ0, θ1 最小极值的解。

范例程序 (房价预测)

手刻线性回归

我们透过 Sklearn 所提供的房价预测资料集进行线性回归模型建模，并采用最小平法。首先为了要验证我们上面的公式，因此我们先利用 Numpy 套件自己手刻做一系列的矩阵运算求出每一项的系数与截距。

import numpy as np
import pandas as pd
from sklearn.metrics import mean_squared_error
from sklearn.datasets import load_boston

# 载入 Sklearn 房价预测资料集 13个输入特徵 1个输出特徵
boston_dataset = load_boston()
# 输入特徵共13个
X = boston_dataset.data
# 设定截距项 b 权重值为 1 
b=np.ones((X.shape[0], 1))
# 添加常数项特徵，最终有 13+1 个输入特徵
X=np.hstack((X, b))
# 输出(房价)
y = boston_dataset.target

# 计算 Beta (@ 为 numpy 中 2-D arrays 的矩阵乘法)
Beta = np.linalg.inv(X.T @ X) @ X.T @ y
y_pred = X @ Beta

# MSE: 21.8948311817292
print('MSE:', mean_squared_error(y_pred, y))

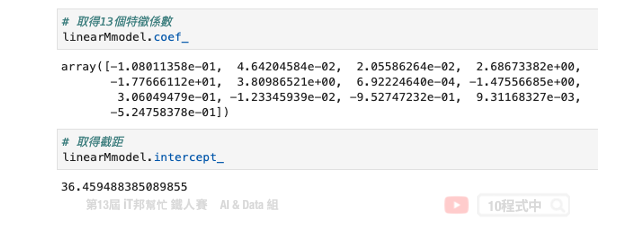
计算出来 Beta 後我们再把所有的 X 带入并做计算，算出来的结果 MSE 为 21.89。最後我们可以试着把 Beta 变数列印出来。总共会有 14 个参数，由 13 个输入特徵系数与最後一项截距所组成的。

输出结果：

array([-1.08011358e-01,  4.64204584e-02,  2.05586264e-02,  2.68673382e+00,
       -1.77666112e+01,  3.80986521e+00,  6.92224640e-04, -1.47556685e+00,
        3.06049479e-01, -1.23345939e-02, -9.52747232e-01,  9.31168327e-03,
       -5.24758378e-01,  3.64594884e+01])

使用 Sklearn LinearRegression

线性回归简单来说，就是将复杂的资料数据，拟和至一条直线上，就能方便预测未来的资料。接下来我们一样使用房价预测资料集，并使用 Sklearn 提供的 LinearRegression 来求解。

Parameters:

• fit_intercept: 是否有截距，如果没有则直线过原点。

Attributes:

• coef_: 取得系数。
• intercept_: 取得截距。

Methods:

• fit: 放入X、y进行模型拟合。
• predict: 预测并回传预测类别。
• score: R2 score 模型评估。

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.datasets import load_boston

# 载入 Sklearn 房价预测资料集 13个输入特徵 1个输出特徵
boston_dataset = load_boston()
# 输入特徵共13个
X = boston_dataset.data
# 输出(房价)
y = boston_dataset.target

# 训练模型
linearModel = LinearRegression()
linearModel.fit(X, y)

y_pred = linearModel.predict(X)
# 21.894831181729202
print('MSE:', mean_squared_error(y_pred, y))

Sklearn 的 LinearRegression 模型也是采用小平方法求解。我们可以发现其 MSE 与稍早手刻的方法相当很接近。另外 Sklearn 模型同时也提供了 coef_ 和 intercept_ 两个属性可以取得模型的特徵系数与截距。

多项式的回归模型

对於线性回归来说，资料都是很均匀地分布在一条直线上，但现实的资料往往是非线性的分布。如果我们一样使用上述方法取得线性模型，在实际场域上预测效果可能并不大。

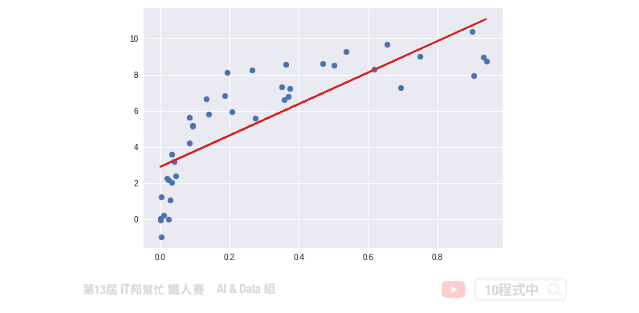
多项式回归中，数据不太具有线性关系，因此应寻找一些非线性曲线去拟合。对於以上的数据，原本是只有一个 x 特徵，但是我们可以建构许多新的特徵。如下图，用一条三次曲线去拟合数据效果更好。我们将三次函数看成 ax3+bx2+cx+d。这样就又变成解多元，其我们就是要找出 a、b、c、d 使其损失函数最小。

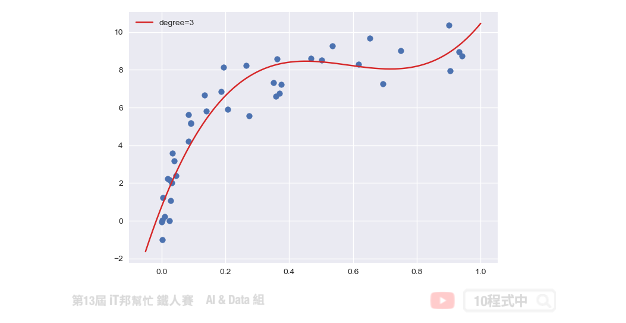
线性模型的扩展

从上述问题中我们可以发现线性回归在实务上所面临的问题。首先我们来回顾一下稍早所提到的线性方程序，这组线性方程序说明了每个特徵 x 一次方与目标值是有一个线性的关系。

y = β0 + β1x1 + β2x2 + ... + βnxn

接着我们再来看一下另一个例子，比如说特徵 x1 与目标值存在着以下的关系。我们发现这组方程序已经不是一个线性关系了，因为他有了 x1 的二次方。

y = β0 + β1x1 + β2x12

那麽该怎麽做我们才能又把它转换成线性关系呢？这时候我们就可以用一个新的特徵 x2。我们让 x2 等於 x1 的平方，这样我们再把 x2 带回原方程序中。此时这两个特徵 x1 与 x2 与目标值又回到了线性关系。

Let x2 = x12

=> y = β0 + β1x1 + β2x2

同样的我们再来看另一个例子。我们如果引入了 x1 的三次方的话，他的方程序如下：

y = β0 + β1x1 + β2x12 + β3x13

同理我们这时一样可以引入新的特徵 x2 等於 x1 的二次方，以及 x3 等於 x1 的三次方。这样经过一个转换以後我们的 y 值与所有的特徵间依然存在着线性关系。

Let x2 = x12 and x3 = x13

=> y = β0 + β1x1 + β2x2 + β3x3

这里做一个小结。我们可以透过引入转变过後的 x 作为一个新的特徵来满足线性假设。此时的回归方程序就是一个多项式回归(polynomial regression)。

Sklearn 实作多项式回归

由於 Sklearn 没有封装好的多项式回归模型可以直接呼叫。不过我们可以透过 make_pipeline 将 PolynomialFeatures 与 LinearRegression 封装成一个多项式回归模型，并且使用者可以随意设定 degree(次方)值。

我们可以对原本的特徵进行 PolynomialFeatures 构造新样本特徵采。并将转换後的特徵送到线性回归模型进行拟合。因此我们可以自定义一个 PolynomialRegression() 的函式，使用者可以输入 degree 大小控制模型的强度。在这个函式中我们使用 Sklearn 的 pipeline 方法将 PolynomialFeatures 特徵转换与 LinearRegression 线性回归模型封装起来。另外以下范例是透过自订义的 make_data() 函式产生一组随机的 x 和 y。该函式中可以设定随机资料的比数，下面程序中我们先随机建立 100 笔数据。

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
plt.style.use('seaborn')

# make_pipeline是指可以将多个Sklearn的function一起执行
def PolynomialRegression(degree=2, **kwargs):
    return make_pipeline(PolynomialFeatures(degree),
                         LinearRegression(**kwargs))

# 随机定义新的x,y值
def make_data(N,err=1,rseed=42):
    rng=np.random.RandomState(rseed)
    x = rng.rand(N,1)**2
    y = 10-1/(x.ravel()+0.1)
    if err>0:
        y+=err*rng.randn(N)
    return x,y

X, y = make_data(100)

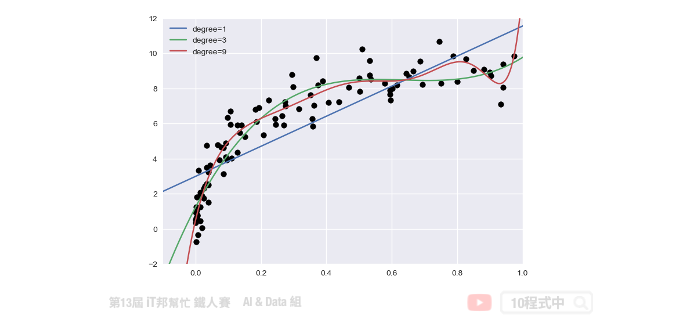
训练资料与测试资料都建立完成後。我们就可以将训练资料丢入建立好的 PolynomialRegression() 并进行数据拟合。下面范例程序中我们演示 degree 等於 1、3、9，并来查看随着次方数的增长对於模型的拟合程度的影响。

# 测试资料集
x_test = np.linspace(-0.1,1.1,500)[:,None]
# 绘制真实答案的分布
plt.scatter(X.ravel(),y,color='black')

# 测试 1,3,7 的degree
for degree in [1,3,9]:
    y_test=PolynomialRegression(degree).fit(X,y).predict(x_test)
    plt.plot(x_test.ravel(),y_test,label='degree={}'.format(degree))
plt.xlim(-0.1,1.0)
plt.ylim(-2,12)
plt.legend(loc='best')

从训练结果可以发现随着次方数 degree 的增长模型会变得越复杂。同时对於训练数据的拟合结果越好。但是这里必须注意并非越大的 degree 就是越好的，因为随着模型复杂会有过度拟合的迹象。因此我们必须找出一个适当的 degree 数值并与测试集验证与评估。目标是训练集与测试集的 MSE 差距要越小越好。如果我们一昧的追求训练集的损失最小化，可能会影响到测试集的表现能力导致预测结果变差。

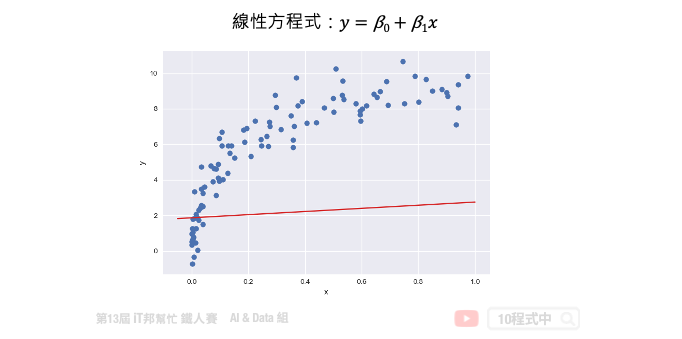
Gradient descent (梯度下降法)

接下来我们来讨论优化问题的第二种方法，就是梯度下降法。梯度下降不仅限於线性回归，在非线性和神经网络同样适用。下图中每一个点是训练集的样本 x 轴为输入值 y 轴为输出值。也就是平面上每个点 x 都会有一个相对应 y 的输出，因此我们需要做的事情是为这些点训练一个模型，使得这条直线能够尽可能反映出 x 与 y 之间的关系。此外我们都知道在一个二维空间中我们能找到无数条直线，那我们该如何找到这条最佳的直线呢？简单来说我们的目标是要使得这些训练资料中的每个样本点到这一条直线的距离平方和要最小。因此这里我们将讨论该如何使用梯度下降法来最佳化我们的模型。首先我们假设一个直线的方程序是 y = β0 + β1x。那首先我们可以先随机的给予 β0 和 β1 一个初始值。并得到下图中的结果，我们可以发现这一条直线并不能反映出 x 和 y 的关联性。

如果我们不断的迭代，每一次的迭代都让这一条直线朝着更符合数据点的方向移动一点，那麽经过许多次的更新我们就可以得到最佳的结果。简单来说就是在每次的迭代要更新所有的参数，例如： β0 和 β1，直到得到最小的 MSE 或是预定的迭代次数。以下的公式就是梯度下降法的表达式。它反映的是每次迭代，我们的 β0 和 β1 这些参数是如何调整的。我们可以从这个公式得知，他是对损失函数求了某一个特定参数的偏导。这就是所谓的梯度，我们朝着梯度的反方向在更新。然而每一次要更新多大可以依靠 η（(eta) 来控制，因此我们算出来的梯度还会乘上一个学习速率来防止更新步伐太大而导致找不到解。所以 η 的大小要适中以免影响到模型最终的收敛。

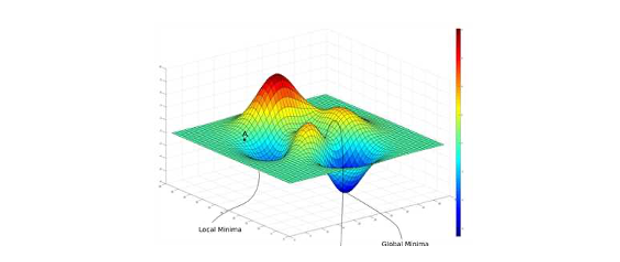
此外这个模型如果透过梯度下降法还有一个缺点，那就是当我们的损失函数不是一个凸函数(convex function) 的时候它就会存在许多个最低点，进而导致在我们选择不同的 β0 和 β1 作为初始值的时候很可能会收敛於不同的局部最佳解(local optimum)。也就是说我们求得的最佳的模型很有机会是局部最佳解而不是全局最佳解(global optimum)。

使用 Sklearn SGDRegressor

Sklearn 提供了 SGDRegressor 并实现了随机梯度下降学习。你可能会问梯度下降与随机梯度下降两者差别在哪？简单来说一般的梯度下降法是一次用全部训练集的数据计算损失函数的梯度，然後做一次参数的更新修正。而随机梯度下降法就是一次跑一个样本或是小批次样本，然後算出一次梯度并更新。而所谓的随机就是在训练过程中随机地抽取样本，所以才会称为随机梯度下降法。

import numpy as np
from sklearn.linear_model import SGDRegressor
from sklearn.metrics import mean_squared_error

# 随机产生一个特徵的X与输出y
X, y = make_data(100)

# 建立 SGDRegressor 并设置超参数
regModel = SGDRegressor(max_iter=100)
# 训练模型
regModel.fit(X, y)
# 建立测试资料
x_test = np.linspace(-0.05,1,500)[:,None]
# 预测测试集
y_test=regModel.predict(x_test)
# 预测训练集
y_pred=regModel.predict(X)
# 视觉化预测结果
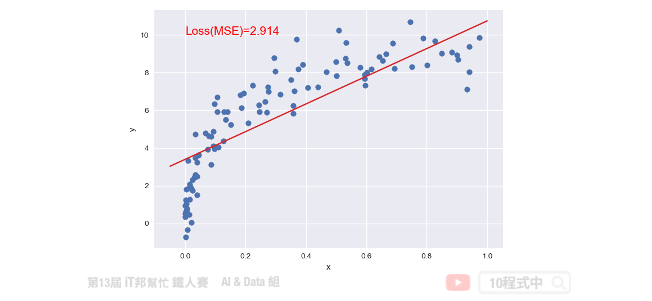
plt.scatter(X,y)
plt.plot(x_test.ravel(),y_test, color="#d62728")
plt.xlabel('x')
plt.ylabel('y')
plt.text(0, 10, 'Loss(MSE)=%.3f' % mean_squared_error(y_pred, y), fontdict={'size': 15, 'color':  'red'})
plt.show()

本系列教学内容及范例程序都可以从我的 GitHub 取得！