IEEE-754 与浮点数运算

本文目标

• IEEE-754
• 规范对於工程发展的重要性
• 认识浮点数
• 使用演算法改善浮点数运算时带来的误差问题

进入正题

在大学的多个课程中都会提到浮点数运算，但大多时候都只是草草带过，为了确保我们能够掌握程序可能出现的特例 (Exception)，认真研究浮点数运算是必须要走的一条路。

IEEE-754

如果说方法/工具是让人能够快速解决问题，那规则就是用来统一方法以避免百家争鸣的状况发生。
电脑科学家在几十年来尝试发展各种在电脑中存放小数的方法，最後则是由 IEEE-754 拿下这一战的胜利，成为被世人广泛接受的浮点数方法。
也因为浮点数方法，我们经常在写程序时碰到奇怪的 Case :

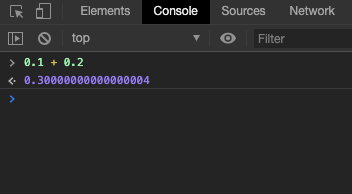
会出现这样的问题并不是电脑的错，而是我们不够了解计算机的行为。

IEEE 二进位浮点数算术标准（IEEE 754）是 20 世纪 80 年代以来最广泛使用的浮点数运算标准，为许多 CPU 与浮点运算器所采用。这个标准定义了表示浮点数的格式（包括负零-0）与反常值（denormal number），一些特殊数值（（无穷（Inf）与非数值（NaN）），以及这些数值的「浮点数运算子」；它也指明了四种数值修约规则和五种例外状况（包括例外发生的时机与处理方式）。
--wikipedia

单精度浮点数

IEEE 754 规范了四种浮点数表达方式，分别是:

• 单精确度
• 双精确度
• 延伸单精确度
• 延伸双精确度

其中，只有单精确度是必备的，其他皆为选择性实作。
基本上，上述四种的剖析方法不会有太大的差异，只是更多的位元能够表达更精确的数值。
因此，本篇文章只会针对单精度浮点数做介绍。

单精度浮点数会占有 32 bits，而这些空间又会被分配成三个部分，分别是:

• sign(1)

1 表示负数，反之代表正数。

• exponent(8)

8 bits 一共可表示 255 种状态，为了有效分配指数为正数和负数的情况，IEEE-754 以 127 表示指数为 0 的情况，若我们今天要表示指数为 3 则变成 3 + 127 = 130。
以 2 进制的方式表示 127 :

    01111111

• fraction(23)

存放小数资料。

将实际资料以浮点数表示

看完上面的介绍不一定能学会浮点数运算，为了避免读者没看懂，让我们来实际操作一次看看:

正规化

以 8.5 为例，若要将它以 IEEE 754 规范的形式表示的话必须先做正规化，也就是将 8.5 拆成 8 + 0.5 再转为 2 进制:

8.5 = 2³ + 1/2¹
2³ + 1/2¹ = 1000.1

最後再让整数部分仅剩个位数 1 : 1.0001 x 2³。

单精度表示

前面已经介绍过单精度浮点数是如何分配 32 个位置，所以我们直接来看要怎麽把 1.0001 x 2³ 存放到 32 bits 的记忆体中吧!

• sign
  因为 8.5 是正数，所以 sign bit 存放 0。
• exponent
  在刚刚，我们得到了 1.0001 x 2³ 的结果，而 exponent 就是 3。
  你认为这样就结束了吗?
  不!刚刚有提到这边以 +127 作为 0，所以要表示 3 我们必须将 127 + 3。因此，我们在这边会在 8 bits 中存放:

  10000010 (130)
  

• fraction
  在处理完 sign 和 exponent 的部分後，我们只要将剩余的小数部分处理就大功告成啦!
  fraction 一共被分配到 23 个 bit，以 8.5 为例，我们仅会存放.0001，所以在记忆体中看起来会像是:

  00010000000000000000000
  

将上面三个部分都处理完成後，在 32-bit 的记忆体模型上看起来就会是这样:

0 10000010 00010000000000000000000

此外，IEEE-754 Floating Point Converter 是一个很棒的小工具，我们可以利用它进行浮点数转换以及查看记忆体模型。

浮点数为什麽叫做浮点数?

关於浮点数的命名由来，我们可以透过维基百科查找其定义:

在计算机科学中，浮点（英语：floating point，缩写为FP）是一种对於实数的近似值数值表现法，由一个有效数字（即尾数）加上幂数来表示，通常是乘以某个基数的整数次指数得到。以这种表示法表示的数值，称为浮点数（floating-point number）。利用浮点进行运算，称为浮点计算，这种运算通常伴随着因为无法精确表示而进行的近似或舍入。
-- wikipedia

因为记忆体有限，若要完整存放多位数的小数(定点数)将会占有非常大的记忆体空间，浮点数算是牺牲准确度换来空间使用率的折衷作法。

浮点数的特例以及如何应对

如何定义一个人很会写程序?除了常见的设计思维、物件导向...，在开发时更会使用相关工具以提升效率或是进行验证 (Git, GDB...)。不过，上述这些东西都不能代表你很会写程序。真正的程序高手是能熟知各种情况下的特例并做出良好的应对处理的，像是: 并不是每个程序开发者都知道程序语言中的小数问题是浮点数规范造成的，更不用说知道如何应对的人更是寥寥可数。

由此可知，笔者也不太会写程序。不过笔者认为:
无知并不可怕，真正可怕的是无知而不自知的人。
这也是为何笔者想藉由撰写文章探讨各种议题的主要原因。

浮点数的特例

在 IEEE-754 中，为了保留正无穷 (exponent = 255) 和负无穷 (exponent = 0)，因此，最大及最小的整数的 exponent 分别是 254 以及 1 :

上图取自维基百科。

从上面的表格中，有可以看到几个浮点数的特例，分别是:

• +-0
  当 exponent 与 fraction 皆为 0，其值为 +-0。

• +-∞
  当 exponent 为 255 且 fraction 为 0，其值为无穷大。

• NaN
  当 exponent 为 255 且 fraction 不为 0，表示 Not a number。此外，根据 IEEE 754 2008 年版本可以得知 NaN 被归类为两种:

  • Quiet NaN
  • Signal NaN

  X111 1111 1AXX XXXX XXXX XXXX XXXX XXXX
  

  我们可以透过从低位数来的第 23 个位元(也就是上面 A 所在的位置) 判断 NaN 的种类，如果在 A 的位置为 1，则为 Quiet NaN，否则为 Signal NaN。
  两者的差别我们也可以从 Intel manual 中得知:

  SNaNs are typically used to trap or invoke an exception handler. They must be inserted by software; that is, the processor never generates an SNaN as a result of a floating-point operation.

  Signal NaN 不会由处理器运算产生且对其做运算会对电脑发出讯号进入异常处理。相反的，Quiet NaN 经由处理器运算後并不会造成程序终止。关於 NaN，可以在 What is the difference between quiet NaN and signaling NaN? 这个问答串中找到网友对两种 NaN 设计的实验:

#include <cassert>
#include <cfenv>
#include <cmath> // isnan
#include <iostream>
#include <limits> // std::numeric_limits
#include <unistd.h>

#pragma STDC FENV_ACCESS ON

int main() {
    float snan = std::numeric_limits<float>::signaling_NaN();
    float qnan = std::numeric_limits<float>::quiet_NaN();
    float f;

    // No exceptions.
    assert(std::fetestexcept(FE_ALL_EXCEPT) == 0);

    // Still no exceptions because qNaN.
    f = qnan + 1.0f;
    assert(std::isnan(f));
    if (std::fetestexcept(FE_ALL_EXCEPT) == FE_INVALID)
        std::cout << "FE_ALL_EXCEPT qnan + 1.0f" << std::endl;

    // Now we can get an exception because sNaN, but signals are disabled.
    f = snan + 1.0f;
    assert(std::isnan(f));
    if (std::fetestexcept(FE_ALL_EXCEPT) == FE_INVALID)
        std::cout << "FE_ALL_EXCEPT snan + 1.0f" << std::endl;
    feclearexcept(FE_ALL_EXCEPT);

    // And now we enable signals and blow up with SIGFPE! >:-)
    feenableexcept(FE_INVALID);
    f = qnan + 1.0f;
    std::cout << "feenableexcept qnan + 1.0f" << std::endl;
    f = snan + 1.0f;

编译并执行上面的程序码便可以取得 exit status:

g++ -ggdb3 -O0 -Wall -Wextra -pthread -std=c++11 -pedantic-errors -o blow_up.out blow_up.cpp -lm -lrt
./blow_up.out
echo $?

• 非正规数
  当 exponent 为 0 且 fraction 不为 0 时，该浮点数为非正规数。用数线来看的话，大概长这样:

  -∞ ~ (sign = 1)最大正规数 ~ -1 ~ (sign = 1)最小正规数 ~ (sign = 1)最大的非正规数 ~ (sign = 1)最小的非正规数 ~ -0/+0 ~ (sign = 0)最小的非正规数 ~ (sign = 0)最大的非正规数 ~ (sign = 0)最小正规数 ~ (sign = 0)最大正规数  ~ +∞
  

  除了规约浮点数，IEEE754-1985标准采用非规约浮点数，用来解决填补绝对值意义下最小规格数与零的距离。（举例说，正数下，最大的非规格数等於最小的规格数。而一个浮点数编码中，如果exponent=0，且尾数部分不为零，那麽就按照非规约浮点数来解析）非规约浮点数源於70年代末IEEE浮点数标准化专业技术委员会酝酿浮点数二进位标准时，Intel公司对渐进式下溢位（gradual underflow）的力荐。当时十分流行的DEC VAX机的浮点数表示采用了突然式下溢位（abrupt underflow）。如果没有渐进式下溢位，那麽0与绝对值最小的浮点数之间的距离（gap）将大於相邻的小浮点数之间的距离。
  -- wikipedia

Kahan Summation

为了节省空间，每次进行浮点数运算都会产生一定的误差值，Kahan 教授为了解决误差问题提出了 Kahan Summation 对每次的浮点运算做补偿以修正这个问题。

准确度与精密度

在学习 Kahan Summation 之前，必须先了解 Precision (准确度) 和 Accuracy (精密度) 的差别。

以 3.14159 为例，如果我们只以小数点後 6 位为标准，我们可以用四个数字诠释准确度与精密度:

• Accurate && Precise
  3.14159
• Accurate && Inprecise
  3.14
• Inaccurate && Precise
  3.14128
• Inaccurate && Inprecise
  3.22

使用更多位元表达浮点数是为了取得更高的准确度，而 Kahan Summation 则是为了修正浮点数运算的精密度误差。

演算法 (虚拟码)

function KahanSum(input)
    var sum = 0.0                    // Prepare the accumulator.
    var c = 0.0                      // A running compensation for lost low-order bits.

    for i = 1 to input.length do     // The array input has elements indexed input[1] to input[input.length].
        var y = input[i] - c         // c is zero the first time around.
        var t = sum + y              // Alas, sum is big, y small, so low-order digits of y are lost.
        c = (t - sum) - y            // (t - sum) cancels the high-order part of y; subtracting y recovers negative (low part of y)
        sum = t                      // Algebraically, c should always be zero. Beware overly-aggressive optimizing compilers!
    next i                           // Next time around, the lost low part will be added to y in a fresh attempt.

    return sum

当有效位数有限且有大数与一个小数做运算时，就会因为能表达的有效位数不足导致後面的数字遗失，例如:

10000.0 + 3.14159 = 10003.14159

假设有效位数为 6，运算结果就会变成:

10000.0 + 3.14159 = 10003.1

Kahan Summation 的作法就是算出这些遗失的值，等到下一轮运算再将他补尝到新的输入当中:

/* 求出误差值 */
c = (10003.1 - 10000.0) - 3.14159 //-0.04159
/* 补偿 */
y = 3.00001 - (-0.04159) //假设下一轮运算的输入是 3.00001

透过 Kahan Summation，在新一轮的输入与上一轮产生的误差值等位时，就可以完全的补偿浮点数运算造成的精密度下降。实际上，Kahan Summation 只能尽可能的补偿误差，如果新一轮的输入与上一轮产生的误差值的大小差距过大，补偿的效果就不会这麽的显着。

Reference

• 从 IEEE 754 标准来看为什麽浮点误差是无法避免的
• 你所不知道的 C 语言: 浮点数运算
• 维基百科
• IEEE 浮点标准详解
• What is the difference between quiet NaN and signaling NaN?
• Kahan summation algorithm